teaching
[courses taught at CMU | courses taught at Columbia | tutorials | interactive demonstrations | miscellaneous]courses taught at CMU
Spring 15
42-732/18-790: Wavelets and multiresolution techniques
Fall 13
42-732/18-790: Wavelets and multiresolution techniques
Spring 13
42-698: Introduction to biomedical signal processing
Fall 12
42-703/18-799: Wavelets and multiresolution techniques
Spring 12
42-540 Introduction to biomedical signal processing
Fall 11
42-201: Professional issues in biomedical engineering
Spring 11
42-540 Introduction to biomedical signal processing
Academic year 09/10
On sabbatical leave
Fall 08
42-201: Professional issues in biomedical engineering
Spring 08
42-703/18-799: Wavelets and multiresolution techniques
Fall 07
42-431/18-496: Bioimaging
Fall 06
42-431/18-496: Bioimaging
42-731/18-795: Advanced bioimaging
42-201: Professional issues in biomedical engineering
Spring 06
42-403/18-496: Bioimaging
Fall 05
42-703/18-795: Advanced bioimaging
Spring 05
42-403/18-496: Bioimaging
Fall 04
42-703/18-799: Advanced bioimaging
Spring 04
2-503/18-799: Advanced signals and biosignal processing with wavelets
Fall 03
Introduction to biosignal processing (informal course)
[courses taught at CMU | courses taught at Columbia | tutorials | interactive demonstrations | miscellaneous]
courses taught at Columbia University
Summer 02
E6860: Wavelets for signal processing and communications
Summer 01
E6860: Wavelets for signal processing and communications
Fall 00
E6860: Wavelets for signal processing and communications
[courses taught at CMU | courses taught at Columbia | tutorials | interactive demonstrations | miscellaneous]
tutorials
Graph Signal Processing Workshop 16
A sampling of sampling for graphs
NORSIG 06
Multiresolution: what, why, how?
[courses taught at CMU | courses taught at Columbia | tutorials | interactive demonstrations | miscellaneous]
interactive demonstrations
These interactive demonstrations are powered by CDF (computable document format) technology. See Wolfram Demonstration Project for more demonstrations and to download a free CDF player.

three vector spaces
Illustration of vectors in various vector spaces. Examples include 2D vectors, sequences and functions. Operations in vectors spaces, addition and scalar multiplication, are illustrated. With the addition of an inner product, a vector space becomes an inner-product space. In particular, the intuitive notion of orthogonality on 2D vectors, when the inner product equals 0, is illustrated in possibly unintuitive settings, such as for sequences and functions.
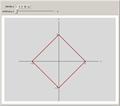
unit-norm vectors under different p norms
Sets of unit-norm vectors for different p-norms: p = 1, p = 2, p = 4, p = 10 and p = infinity. Vectors ending on the lines are of unit norm in the corresponding p-norm.

a pair of biorthogonal bases in the real plane
A pair of biorthogonal bases in the real plane. The basis (black) and its dual basis (red) are given when they exist (when matrices are invertible).
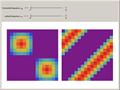
separable and nonseparable 2D sequences
Illustration of a separable 2D sinusoidal sequence (left) versus the nonseparable one (right). The separable sequence can only achieve rectangular space patterns, while the nonseparable one offers more freedom. The image size is 16x16.
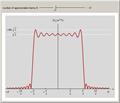
Gibbs phenomenon in the truncated DTFT of the sinc sequence
The Gibbs phenomenon refers to the oscillations around a discontinuity in a function when trying to represent it with a Fourier series using only a finite number of terms. Here we show the same phenomenon on the discrete-time Fourier transform (DTFT) of a sinc sequence. Using only a finite number of terms to compute the DTFT leads to the Gibbs phenomenon. The oscillations around the discontinuity persist with the amplitude of roughly 9% of the original height.
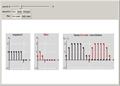
equivalence of linear and circular convolutions
This Demonstration studies the equivalence of linear and circular convolutions. In signal processing, linear convolution (or simply convolution) refers to the convolution between infinitely supported sequences and filters, while circular convolution refers to the convolution between finitely-supported sequences and filters, circularly extended.
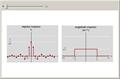
ideal Nth-band discrete filters
Impulse and magnitude responses of ideal Nth-band lowpass discrete filters for N=2, 3, ..., 9. While such filters are not realizeable, they serve as a desired template for passing certain frequencies while blocking others. The impulse response of an ideal lowpass filter is a sinc sequence (of unit norm in the figure) while its magnitude response is constant in the passband.
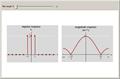
moving-average discrete filters
Impulse and magnitude responses of a moving-average discrete filter for N = 3, 5, 7, 9, 11. Such a filter can be used to smooth variations present in a sequence and obtain a global trend.

linear-phase discrete filters
Impulse and magnitude responses of linear-phase discrete filters. Such filters have constant group delay, which means that all the frequency components are delayed by the same amount, a property desirable in many applications. The impulse response of a linear-phase discrete filter is either symmetric or antisymmetric.
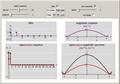
multirate signal processing: downsampling
This Demonstration shows the effect of filtering followed by downsampling (sometimes also called subsampling or decimation) on a discrete-time sequence and its discrete-time Fourier transform (DTFT) spectrum. Downsampling by a factor of N removes every Nth sample from a discrete-time sequence. This contraction in time results in an expansion in frequency, necessitating filtering prior to downsampling.
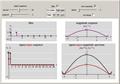
multirate signal processing: upsampling
This Demonstration shows the effect of upsampling followed by filtering on a discrete-time sequence and its discrete-time Fourier transform (DTFT) spectrum. Upsampling by a factor of N inserts N zeros between every two samples of a discrete-time sequence. This expansion in time causes a contraction in frequency and the appearance of spurious spectral components, necessitating filtering after upsampling.

twin-dragon wavelet
This Demonstration shows the iteration process that approximates a continuous-time, "twin dragon" wavelet basis, from the discrete-time one. The iteration is performed on the so-called "quincunx" lattice. At every itertation, the resulting function tiles the space, even though it has a "fractal" boundary.
[courses taught at CMU | courses taught at Columbia | tutorials | interactive demonstrations | miscellaneous]
miscellaneous
Useful tables from Foundations of Signal Processing [download]
Fundamental subspaces associated with matrix A
Discrete-time processing concepts
Multirate discrete-time processing concepts
Kronecker delta sequence and Dirac delta function properties
Ideal filters, box and sinc functions and sequences
Energy, power and orthogonality concepts for sequences
Deterministic discrete-time autocorrelation/crosscorrelation properties
Discrete-time Fourier transform (DTFT) properties
Discrete Fourier transform (DFT) properties
Fourier transform properties
Fourier series properties
Discrete/continuous Fourier transform summary
z-transform properties
[courses taught at CMU | courses taught at Columbia | tutorials | interactive demonstrations | miscellaneous]